Representation of a 3d vector. More...
#include <Matrix4x4.h>
Public Member Functions | |
| Vector3 () | |
| Vector3 (T _x, T _y, T _z) | |
| Vector3 (const Vector3< T > &other)=default | |
| Vector3 (Vector3< T > &&other) noexcept=default | |
| double | DotProduct (const Vector3< T > &other) const |
| Will compute the dot product to another Vector3. More... | |
| Vector3< double > | CrossProduct (const Vector3< T > &other) const |
| Will compute the cross product to another Vector3. More... | |
| double | SqrMagnitude () const |
| Will compute the square magnitude. More... | |
| double | Magnitude () const |
| Will compute the magnitude. More... | |
| Vector3< double > | Normalize () const |
| Will return the normalization of this vector. More... | |
| void | NormalizeSelf () |
| Will normalize this vector. More... | |
| Vector3< T > | VectorScale (const Vector3< T > &scalar) const |
| Will scale self.n by scalar.n. More... | |
| void | LerpSelf (const Vector3< T > &other, double t) |
| Will lerp itself towards other by t. More... | |
| Vector3< double > | Lerp (const Vector3< T > &other, double t) const |
| Will return a lerp result between this and another vector. More... | |
| bool | Similar (const Vector3< T > &other, double epsilon=0.00001) const |
| Will compare if two vectors are similar to a certain epsilon value. More... | |
| Vector3< int > | ToInt () const |
| Will convert this vector to a Vector3i. More... | |
| Vector3< double > | ToDouble () const |
| Will convert this vector to a Vector3d. More... | |
| T & | operator[] (std::size_t idx) |
| const T & | operator[] (std::size_t idx) const |
| Vector3< T > | operator+ (const Vector3< T > &other) const |
| void | operator+= (const Vector3< T > &other) |
| Vector3< T > | operator- (const Vector3< T > &other) const |
| void | operator-= (const Vector3< T > &other) |
| Vector3< T > | operator* (const T scale) const |
| void | operator*= (const T scale) |
| Vector3< T > | operator/ (const T scale) const |
| void | operator/= (const T scale) |
| Vector3< T > | operator* (const Matrix4x4 &mat) const |
| void | operator*= (const Matrix4x4 &mat) |
| Vector3< T > | operator- () const |
| operator Vector2< T > () const | |
| operator Vector4< T > () const | |
| Conversion method. More... | |
| void | operator= (const Vector3< T > &other) |
| Conversion method. More... | |
| void | operator= (Vector3< T > &&other) noexcept |
| bool | operator== (const Vector3< T > &other) const |
| bool | operator!= (const Vector3< T > &other) const |
Public Attributes | |
| T | x |
| T | y |
| T | z |
Static Public Attributes | |
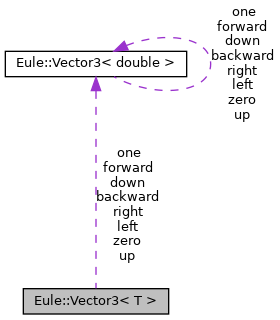
| static const Vector3< double > | up |
| static const Vector3< double > | down |
| static const Vector3< double > | right |
| static const Vector3< double > | left |
| static const Vector3< double > | forward |
| static const Vector3< double > | backward |
| static const Vector3< double > | one |
| static const Vector3< double > | zero |
Friends | |
| std::ostream & | operator<< (std::ostream &os, const Vector3< T > &v) |
| std::wostream & | operator<< (std::wostream &os, const Vector3< T > &v) |
Detailed Description
template<typename T>
class Eule::Vector3< T >
Representation of a 3d vector.
Contains a lot of utility methods.
Definition at line 9 of file Matrix4x4.h.
Constructor & Destructor Documentation
◆ Vector3() [1/4]
|
inline |
◆ Vector3() [2/4]
|
inline |
◆ Vector3() [3/4]
|
default |
◆ Vector3() [4/4]
|
defaultnoexcept |
Member Function Documentation
◆ CrossProduct()
Will compute the cross product to another Vector3.
Definition at line 68 of file Vector3.cpp.
◆ DotProduct()
| double Vector3::DotProduct | ( | const Vector3< T > & | other | ) | const |
◆ Lerp()
| Vector3< double > Vector3::Lerp | ( | const Vector3< T > & | other, |
| double | t | ||
| ) | const |
Will return a lerp result between this and another vector.
Definition at line 330 of file Vector3.cpp.
◆ LerpSelf()
| void Vector3::LerpSelf | ( | const Vector3< T > & | other, |
| double | t | ||
| ) |
Will lerp itself towards other by t.
Definition at line 311 of file Vector3.cpp.
◆ Magnitude()
| double Vector3::Magnitude |
Will compute the magnitude.
Definition at line 95 of file Vector3.cpp.
◆ Normalize()
| Vector3< double > Vector3::Normalize |
Will return the normalization of this vector.
Definition at line 147 of file Vector3.cpp.
◆ NormalizeSelf()
| void Vector3::NormalizeSelf | ( | ) |
Will normalize this vector.
Definition at line 200 of file Vector3.cpp.
◆ operator Vector2< T >()
| Vector3::operator Vector2< T > |
Definition at line 873 of file Vector3.cpp.
◆ operator Vector4< T >()
| Vector3::operator Vector4< T > |
Conversion method.
Definition at line 879 of file Vector3.cpp.
◆ operator!=()
| bool Vector3::operator!= | ( | const Vector3< T > & | other | ) | const |
Definition at line 864 of file Vector3.cpp.
◆ operator*() [1/2]
Definition at line 731 of file Vector3.cpp.
◆ operator*() [2/2]
| Vector3< T > Vector3::operator* | ( | const T | scale | ) | const |
Definition at line 541 of file Vector3.cpp.
◆ operator*=() [1/2]
| void Vector3::operator*= | ( | const Matrix4x4 & | mat | ) |
Definition at line 836 of file Vector3.cpp.
◆ operator*=() [2/2]
| void Vector3::operator*= | ( | const T | scale | ) |
Definition at line 583 of file Vector3.cpp.
◆ operator+()
Definition at line 372 of file Vector3.cpp.
◆ operator+=()
| void Vector3::operator+= | ( | const Vector3< T > & | other | ) |
◆ operator-() [1/2]
| Vector3< T > Vector3::operator- |
Definition at line 806 of file Vector3.cpp.
◆ operator-() [2/2]
Definition at line 456 of file Vector3.cpp.
◆ operator-=()
| void Vector3::operator-= | ( | const Vector3< T > & | other | ) |
◆ operator/()
| Vector3< T > Vector3::operator/ | ( | const T | scale | ) | const |
Definition at line 626 of file Vector3.cpp.
◆ operator/=()
| void Vector3::operator/= | ( | const T | scale | ) |
Definition at line 667 of file Vector3.cpp.
◆ operator=() [1/2]
| void Vector3::operator= | ( | const Vector3< T > & | other | ) |
◆ operator=() [2/2]
|
noexcept |
◆ operator==()
| bool Vector3::operator== | ( | const Vector3< T > & | other | ) | const |
◆ operator[]() [1/2]
| T & Vector3::operator[] | ( | std::size_t | idx | ) |
Definition at line 235 of file Vector3.cpp.
◆ operator[]() [2/2]
| const T & Vector3::operator[] | ( | std::size_t | idx | ) | const |
Definition at line 251 of file Vector3.cpp.
◆ Similar()
| bool Vector3::Similar | ( | const Vector3< T > & | other, |
| double | epsilon = 0.00001 |
||
| ) | const |
Will compare if two vectors are similar to a certain epsilon value.
Definition at line 213 of file Vector3.cpp.
◆ SqrMagnitude()
| double Vector3::SqrMagnitude | ( | ) | const |
◆ ToDouble()
| Vector3< double > Vector3::ToDouble |
Will convert this vector to a Vector3d.
Definition at line 229 of file Vector3.cpp.
◆ ToInt()
| Vector3< int > Vector3::ToInt |
Will convert this vector to a Vector3i.
Definition at line 223 of file Vector3.cpp.
◆ VectorScale()
Will scale self.n by scalar.n.
Definition at line 135 of file Vector3.cpp.
Friends And Related Function Documentation
◆ operator<< [1/2]
|
friend |
◆ operator<< [2/2]
|
friend |
Member Data Documentation
◆ backward
|
static |
◆ down
|
static |
◆ forward
|
static |
◆ left
|
static |
◆ one
|
static |
◆ right
|
static |
◆ up
|
static |
◆ x
| T Eule::Vector3< T >::x |
◆ y
| T Eule::Vector3< T >::y |
◆ z
| T Eule::Vector3< T >::z |
◆ zero
|
static |
The documentation for this class was generated from the following files:
- Eule/Matrix4x4.h
- Eule/Vector3.h
- Eule/Vector3.cpp
 1.8.17
1.8.17